10/7/16 - Conservation of Mass and Momentum

A cube made of wire is sitting in the wind. The wind is calm and steady. In these conditions, we know exactly how much air is moving into and out of the cube and how fast this is happening. Mass and momentum must be conserved.

The conservations of mass and momentum can help us analyze flows through a conservation-based perspective. If we know what the properties of the flow are entering a specific control area, we also know we can expect them to be at the exit.

Let's look at an example flow.

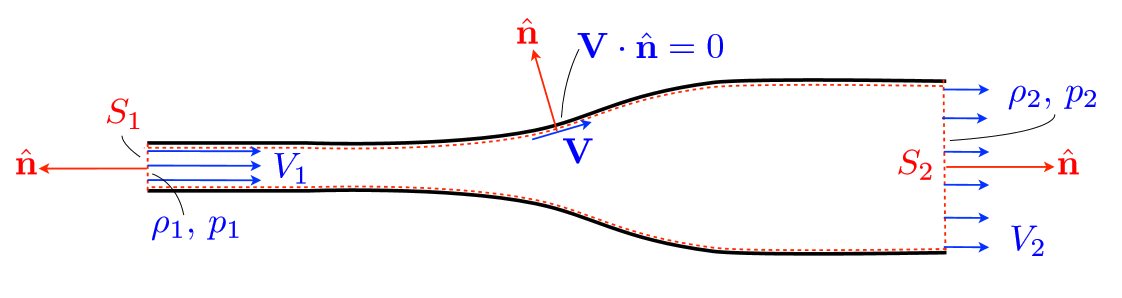
At the beginning of the control volume, the flow has a velocity of \(V_1\), a density of \(\rho_1\), and a pressure of \(p_1\). As the volume widens, the fluid follow the edges (\(\rm{V \cdot \hat{n}=0}\), meaning flow is parallel to the side of the control volume) and expands into the greater cross-sectional area. When the cross-sectional volume increases, something about the flow must change. The flow could, according to the conservation of momentum, slow down. The amount of momentum passing through each unit area is lower, but the area of the cross section has increased. The flow might keep the same velocity but have a lower pressure. Maybe the density changes.

These three variables will change based on the geometry of the flow, but they are related. How are they related? $$\rho_1 p_1 V_1 = \rho_2 p_2 V_2$$ This equation is relieving to see. It perfectly represents how the density, pressure, and velocity of a flow are related to one another while not being confusing or complicated.


--Aryn Harmon