
stumbling into aerodynamics
Home Posts About Me

Lift is not a force generally well understood. Many people have misconceptions (including me) about what exactly lifts bodies in aerodynamic flows. Air flowing around objects most definitely influences their position in space, but how does it do this? We can give the simple explanation in terms of Bernoulli's principle.
As air flows around the wing, it takes one of two basic paths: over the wing or under the wing. The air which moves over the wing speeds up because of the larger distance to travel. The diagram below illustrates this.
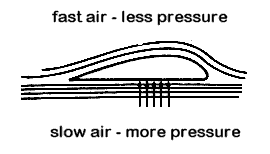
According to Bernoulli's principle, the air's pressure falls as it speeds up. This creates a pressure differential which contributes lift, but is not the main source.
Lift is mainly generated by flow turning. This is the result of the conservation of momentum and Newton's third law. Unsurprisingly, we need to think about one of the most important equations in physics,
$$\vec{F}=m\vec{a}$$
A force in once direction is equal to a mass times its acceleration in the same direction. In order to be forced upwards, the wing must exert a downwards force on the air flowing around it. According to the conservation of momentum which we discussed earlier, the change in momentum in the air, the turning of the flow, must be balanced by the change in the momentum of the wing if there are no external forces. In most analyses, the air enters the control volume (CV) without being perturbed and approaches the wing in a straight path. (This is an assumption to make calculations easier.) The flow leaves the CV with a \(\rm -\hat{j}\) (downwards) velocity.
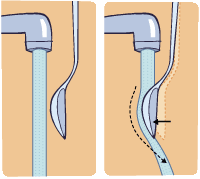
A Spoon in a Water Flow

This airfoil has a small angle of attack, but it is still clear that the flow lines turn downwards in the negative streamwise direction.
The scope of the CV in this animation is not ideal as it does not extend far enough in front of the airfoil for the air to enter perfectly level. We should use this image to understand how the flow turns downwards.
This is the whole series of terms which describes conservation of momentum in a control volume.
$$\int \hspace{-1.7ex} \int \hspace{-1.7ex} \int _{\cal V}\frac{\partial }{\partial t}\left(\rho {\bf V}\right)\, {\rm d}{\cal V}+ \int \hspace{-1.7ex} \int _{S} \rho {\bf V}\, {\bf V}\cdot \hat{{\bf n}}\, {\rm d}S = \int \hspace{-1.7ex} \int \hspace{-1.7ex} \int _{{\cal V}} \rho {\bf g}\, {\rm d}{\cal V}-\int \hspace{-1.7ex} \int _{S} p\, \hat{{\bf n}}\, {\rm d}S +\int \hspace{-1.7ex} \int _{S} \boldsymbol {\tau }\, {\rm d}S + \sum {\bf F}_{\rm ext}$$
or in conceptual terms,
(rate of change of mass in CV) + (all momentum flowing in/out) =
(gravitation forces) - (pressure forces) + (torsion forces) + (external forces)
--Aryn Harmon